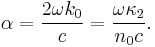Franz–Keldysh effect and modulation spectroscopy

Contents

Introduction

The absorption coefficient is related to the dielectric constant (especially complex term). From Maxwell's equation, we can easily find out the relation,

\alpha = \frac{2\omega k_0} {c}={{\omega\kappa_2} \over{n_0c}}.

We will consider the direct transition of an electron from the valence band to the conduction band induced by the incident light in a perfect crystal and try to take into account of the change of absorption coefficient for each Hamiltonian with a probable interaction like electron-photon, electron-hole, external field. These approach follows from.[1] We put the 1st purpose on the theorical background of Franz–Keldysh effect and third-derivative modulation spectroscopy.

One electron Hamiltonian with EM (electro magnetic) field

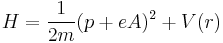H = {1 \over 2m} (p%2BeA)^2 %2B V(r) (A: vector field, V(r): periodic potential)

A = {1 \over 2} A_0 e [e^{i(k_p \cdot r - \omega t)}%2Be^{-i(k_p \cdot r - \omega t)}] (k_p and e are the wave vector of em field and unit vector.)

And neglecting the square term 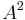A^2, using the relation A \cdot p = p \cdot A ,

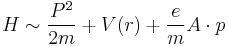
H \sim {P^2 \over 2m} %2B V(r) %2B {e \over m} A \cdot p

Then using the Bloch function 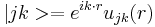|jk> = e^{ik \cdot r} u_{jk}(r) (j= v, c that mean valence band, conduction band)

the transition probability can be obtained such that

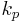w_{cv} = {2 \pi \over \hbar}^2 |<ck'| {e \over m} A \cdot p |vk>|^2\delta[\Epsilon _c (k') - \Epsilon _v (k) - \hbar \omega] = {\pi e^2 \over 2 \hbar m^2}A_0 ^2 |<ck'|exp(ik_p \cdot r)e \cdot p |vk>|^2 \delta[\Epsilon _c (k') - \Epsilon _v (k) - \hbar \omega](k_pmeans wave vector of light)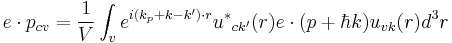 e \cdot p_{cv} = {1 \over V} \int_v e^{i(k_p %2Bk-k') \cdot r} {u^*}_{ck'}(r)e \cdot (p%2B \hbar k)u_{vk} (r) d^3r

Power dissipation of the electromagnetic waves per unit time and unit volume gives rise to following equation

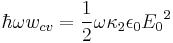
\hbar \omega w_{cv} = {1 \over 2} \omega \kappa_2 \epsilon_0 {E_0}^2

From the relation between the electric field and the vector potential, 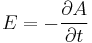{E} = -{{\partial A} \over {\partial t}}, we may put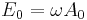 E_0 = \omega A_0

And finally we can get the imaginary part of the dielectric constant and surely the absorption coefficient. \kappa = {{\pi e^2} \over {\epsilon_0 m^2 \omega^2}}\sum_{k,k'} |e \cdot p_{cv}|^2 delta[\Epsilon _c (k') - \Epsilon _v (k) - \hbar \omega]\delta_{kk'}

2-body(electron-hole) Hamiltonian with EM field

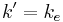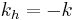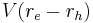An electron in the valence band(wave vector k) is excited by photon absorption into the conduction band(the wave vector at the band is k'=k_e) and leaves a hole in the valence band(the wave vector of the hole is k_h=-k). In this case, we include the electron-hole interaction.(V(r_e -r_h))

Thinking about the direct transition, 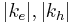|k_e|, |k_h| is almost same. But Assume the slight difference of the momentum due to the photon absorption is not ignored and the bound state- electron-hole pair is very week and the effective mass approximation is valid for the treatment. Then we can make up the following procedure, the wave function and wave vectors of the electron and hole

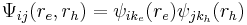\Psi_{ij} (r_e, r_h) = \psi_{ik_e}(r_e) \psi_{jk_h} (r_h) (i, j are the band indices, and re, rh, ke, kh are the coordinates and wave vectors of the electron and hole respectively)

And we can take a total wave vector K such that

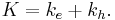
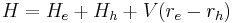
K = k_e %2B k_h. H=H_e %2B H_h %2BV(r_e -r_h)

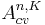
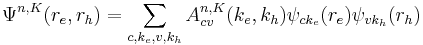
Then, Bloch functions of the electron and hole can be constructed with the phase term A^{n,K}_{cv} \Psi^{n,K}(r_e,r_h) = \sum_{c,k_e,v,k_h}A^{n,K}_{cv}(k_e,k_h) \psi_{ck_e}(r_e) \psi_{vk_h} (r_h)

If V slowly over the distance of the integral, the term can be treated like following.

[\Epsilon_c(k_e) %2B \Epsilon_h(k_h)%2BV(r_e-r_h)-\epsilon]A^{n,K}_{c,V}(k_e,k_h) =0(*)

here we assume that the conduction and valence bands are parabolic with scalar masses and that at the top of the valence band 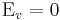\Epsilon_v =0, i.e. 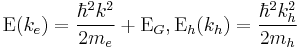\Epsilon(k_e) = {{\hbar^2k^2} \over {2m_e}}%2B\Epsilon_G, \Epsilon_h(k_h)={{\hbar^2k_h^2} \over {2m_h}} (\EpsilonG is the energy gap)

Now, The Fourier transform of 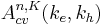A^{n,K}_{cv}(k_e,k_h) and above (*), the effective mass equation for the exciton may be written as

[(-{\hbar^2 \over 2M}\nabla^2)%2B(-{\hbar^2 \over 2\mu} \nabla^2-{e^2 \over 4\pi\epsilon r})]\Phi^{n,k}(r,R) = [\epsilon-\epsilon G] \cdot \Phi^{n,K}(r,R)

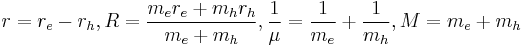
r=r_e-r_h, R={{m_e r_e %2B m_h r_h}\over {m_e%2Bm_h}}, {1 \over \mu} = {1\over m_e}%2B{1 \over m_h}, M= m_e %2B m_h

then the solution of eq is given by

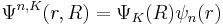
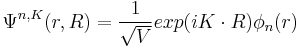
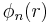\Psi^{n,K} (r,R) = \Psi_K(R)\psi_n(r) \Psi^{n,K} (r,R) = {1 \over \sqrt {V}}exp(iK \cdot R) \phi_n(r) \phi_n(r) is called the envelope function of an exciton. The ground state of the exciton is given in analogy to the hydrogen atom.

then, the dielectric function is

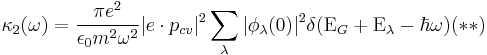
\kappa_2(\omega) = {\pi e^2 \over{\epsilon_0 m^2 \omega^2}} |e \cdot p_{cv}|^2\sum_{\lambda} |\phi_\lambda(0)|^2 \delta(\Epsilon_G %2B \Epsilon_\lambda - \hbar\omega)(**)

detailed calculation is in.[1]

Franz–Keldysh effect

Franz–Keldysh effect means an electron in a valence band can be allowed to be excited into a conduction band by absorbing a photon with its energy below the band gap. Now we're thinking about the effective mass equation for the relative motion of electron hole pair when the external field is applied to a crystal. But we are not to take a mutual potential of electron-hole pair into the Hamiltonian.

When the Coulomb interaction is neglected, the effective mass equation is

[-{\hbar^2 \over 2\mu} \nabla^2 - eE \cdot r ] \psi(r) = \epsilon \psi(r).

And the equation can be expressed,

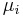[-{\hbar^2 \over 2\mu}{d^2 \over {dr_i^2}}-eE_ir_i-\epsilon_i]\psi(r_i) = 0( where \mu_i is the value in the direction of the principal axis of the reduced effective mass tensor)

Using change of variables:

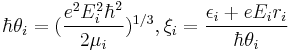
\hbar\theta_i = ({{e^2E_i^2\hbar^2} \over {2\mu_i}})^{1/3}, \xi_i={{\epsilon_i%2BeE_ir_i}\over{\hbar\theta_i}}

then the solution is

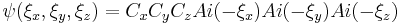
\psi(\xi_x,\xi_y,\xi_z)=C_x C_y C_z Ai(-\xi_x)Ai(-\xi_y)Ai(-\xi_z)

where 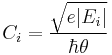C_i = {{\sqrt{e|E_i|}}\over{\hbar\theta}}

For example, 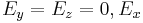E_y=E_z=0, E_x the solution is given by

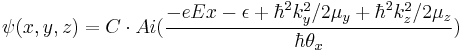
\psi(x,y,z)=C \cdot Ai({{-eEx-\epsilon%2B\hbar^2k_y^2/2\mu_y %2B \hbar^2k_z^2/2\mu_z} \over {\hbar\theta_x}})

The dielectric constant can be obtained inserting this equation to the (**) (above block), and changing the summation with respect to λ to 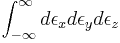\int_{-\infty}^{\infty}d\epsilon_xd\epsilon_yd\epsilon_z

The integral with respect to 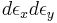d\epsilon_x d\epsilon_y is given by the joint density of states for the two-D band. (the Joint density of states is nothing but the meaning of DOS of both electron and hole at the same time.)

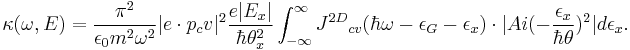
{\kappa(\omega, E)} = {{\pi^2} \over{\epsilon_0 m^2 \omega^2}}|e \cdot p_cv|^2 {{e|E_x|} \over {\hbar\theta_x^2}}\int_{-\infty}^{\infty}{J^{2D}}_{cv}(\hbar\omega - \epsilon_G - \epsilon_x) \cdot|Ai(-{{\epsilon_x} \over {\hbar\theta}})^2 |d\epsilon_x.

where 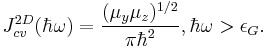J^{2D}_{cv}(\hbar\omega) = {(\mu_y\mu_z)^{1/2} \over \pi\hbar^2}, \hbar\omega > \epsilon_G.

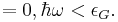
=0, \hbar\omega < \epsilon_G.

Then we put 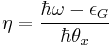\eta = {{\hbar\omega - \epsilon_G} \over {\hbar\theta_x}}

And think about the case we find 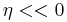\eta<<0 , thus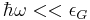\hbar\omega << \epsilon_G with the asymptotic solution for the Airy function in this limit.

Finally ,\kappa _2(\omega, E_x) = {1/2}\kappa_2(\omega)exp[{-4 \over 3}({{\epsilon_G-\hbar\omega} \over {\hbar\theta_x}})]

Therefore the dielectric function for the incident photon energy below the band gap is exist! These results indicate that absorption occurs for an incident photon.

Modulation spectroscopy

In physical system, we can find out the useful physical information of it using small modulation to probe. In Optics, we can make an experimental derivative to the wavelength of incident ray, the E field to the sample, temperature, pressure, uniaxial stress etc. for getting more physical property. We can generally call them modulation spectroscopy. This method is often referred to as electroreflectance or electroabsorption because small modulation lead to the change of reflectance at last.

Here we focus on the theory of third derivative form of Aspnes cites often as third-derivative modulation spectroscopy.

References

  1. ^ a b C. Hamaguchi, "Basic Semiconductor Physics", Springer (2001)